

1-2 算数繰り上がりのあるたし算
3校時,1年2組では算数を勉強していました。今取り組んでいるのは繰り上がりのあるたし算です。前時は9+3を学習しました。足される数の9はあと1で十のまとまりになるのでたす数の3を1と2に分け,9と1で10,10と残りの2を足して12と答えを求めます。
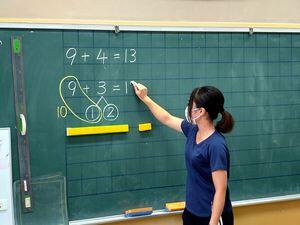

担任のS先生が板書しているのが,いわゆる「サクランボ計算」で,足す数を1と2に分けるとサクランボのようだから,こう呼ぶようです。子どもたちはブロック操作でも,その過程を確かめました。
さて,今日の学習は8+3の計算です。足される数が9から8に変わりました。


先ずはブロック操作で答えを求めてみます。Rくんが黒板で操作してくれました。
その後,S先生は「3をいくつといくつに分けますか?」「なぜ2と1に分けたのですか?」と問うて行きます。Kさんは「8はあと2で十のまとまりになるから,2と1に分けます。」と発表しました。他のみんなもそのことに気付きました。それをサクランボ計算にも表していきます。

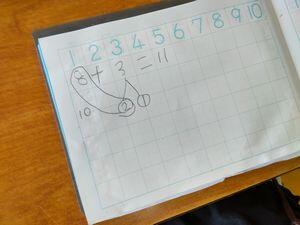
類題を解くうちに,8+いくつのたしざんでは2といくつのサクランボを作ればいいことを確かなものにしていきます。同時に9と1,8と2と補数も意識していきます。
その様子を見極めて,S先生は発展問題として7+4の問題を出しました。ほとんどの子どもたちは3と1のサクランボだとすぐに気付きます。S先生のまる付けを待っていたようなので,私からのスペシャル問題6+5を出しました。さて,できたでしょうか?正解した子には「山田マーク」をノートに書きましたので,確かめてみてください。
ちなみに,S先生は明日,初任研に先輩教師として参加し,この前の時間の授業の様子を紹介します。頑張って!
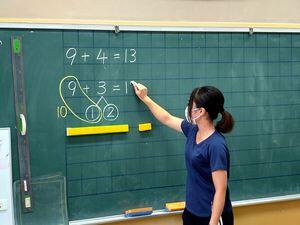

担任のS先生が板書しているのが,いわゆる「サクランボ計算」で,足す数を1と2に分けるとサクランボのようだから,こう呼ぶようです。子どもたちはブロック操作でも,その過程を確かめました。
さて,今日の学習は8+3の計算です。足される数が9から8に変わりました。


先ずはブロック操作で答えを求めてみます。Rくんが黒板で操作してくれました。
その後,S先生は「3をいくつといくつに分けますか?」「なぜ2と1に分けたのですか?」と問うて行きます。Kさんは「8はあと2で十のまとまりになるから,2と1に分けます。」と発表しました。他のみんなもそのことに気付きました。それをサクランボ計算にも表していきます。

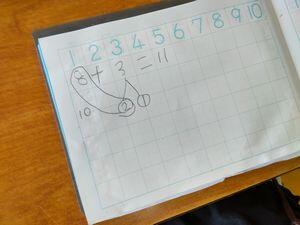
類題を解くうちに,8+いくつのたしざんでは2といくつのサクランボを作ればいいことを確かなものにしていきます。同時に9と1,8と2と補数も意識していきます。
その様子を見極めて,S先生は発展問題として7+4の問題を出しました。ほとんどの子どもたちは3と1のサクランボだとすぐに気付きます。S先生のまる付けを待っていたようなので,私からのスペシャル問題6+5を出しました。さて,できたでしょうか?正解した子には「山田マーク」をノートに書きましたので,確かめてみてください。
ちなみに,S先生は明日,初任研に先輩教師として参加し,この前の時間の授業の様子を紹介します。頑張って!
2
4
4
6
8
0
7
ブログ
面瀬小ニュース
記事がありません。
連絡先
宮城県気仙沼市松崎下赤田58番地
TEL 0226-22-7800
FAX 0226-24-7215
omose-sho◎kesennuma.ed.jp
(迷惑メール防止のため@マークを◎にしています)
学校周辺の地図
QRコード

